Home Was ist ot ? Regeln Mitglieder Maintainer Impressum FAQ/Hilfe
4.4. Lernkonzepte in Theorien »Neuronaler Netze«
Maintainer: Stefan Meretz, Version 1, 14.02.2004
Projekt-Typ: halboffen
Status: Archiv
(1) Wir haben in den vorstehenden Teilkapiteln behavioristische Lerntheorien und kognitivistische Gedächtnistheorien deshalb dargestellt, weil sich die »Neuronetztheorien« darauf beziehen und dabei festgestellt, daß die behavioristische SR-Theorie menschliches Lernen nur in seiner Außendetermination durch isolierte Reizquellen erfassen kann. Wir haben diese Form des Lernens als induktives Lernen bzw. als Lernen unter Zwang bezeichnet, da das Subjekt aufgrund begrenzter Zugangsmöglichkeiten zur Welt lediglich zufällige Regelhaftigkeiten von Ereignisfolgen lernt. Dabei haben wir hervorgehoben, daß sich die Reduktion sachlich-sozialer Bedeutungszusammenhänge auf isolierte Einzelereignisse als Gegebenheitszufälle schon aus den verwendeten Grundbegriffen ergibt. In der kognitivistischen Gedächtnisforschung werden lediglich solche Lernaktivitäten thematisiert, in denen das Individuum die Dauerhaftigkeit seiner Lernresultate anstrebt - einem Spezialfall der Lernforschung. Während in der SR-Theorie jedoch noch sachlich-soziale Bedeutungszusammenhänge in Form von isolierten Gegebenheitszufällen berücksichtigt sind, werden diese hier völlig ausgeklammert. Damit einher geht auch eine verschleiernde Hineinverlagerung des Subjekts in das System, indem der Computer von einem Hilfsmittel in ein Modell menschlicher Kognition umgedeutet wird. Subjekte werden in Termini des Systems modelliert, womit ihr Platz außerhalb des von ihnen geschaffenen Systems verlorengeht und das System zum »selbsttätigen Agenten« seiner eigenen Operationen wird. Beide Strömungen bilden Bezugspunkte konnektionistischer »Lernverfahren«. Das bedeutet, daß sich die prinzipiellen Beschränkungen von SR-Theorie und kognitivistischer Gedächtnisforschung in diesen Verfahren niederschlagen. Dies wollen wir in der folgenden Darstellung dieser »Lernverfahren« genauer ausführen. Wir beschränken uns dabei auf einige wesentliche Verfahren, die für uns exemplarischen Charakter besitzen. Wir beziehen uns in unserer Darstellung in der Regel auf zusammenfassende Veröffentlichungen, so Brause (1991), Hecht-Nielsen (1990), Hertz et al. (1991), Kratzer (1990), Lawrence (1992), McClelland und Rumelhart (1986), Ossen (1990), Ritter et al. (1990), Rojas (1993), Rumelhart und McClelland (1986), ohne diese immer explizit anzuführen.
(2) Zentraler Ansatzpunkt der »Neuronetztheorien« ist die Vorstellung, durch Modellierung der Substrukturen des Gehirns von Tieren und Menschen eine vergleichbare Leistungsfähigkeit auf computertechnischem Wege zu erzielen. Aus diesem Grund finden sich in nahezu allen einschlägigen Lehrbüchern sowie Überblicksdarstellungen zu »Neuronalen Netzen« Einführungen in die Neurobiologie und -physiologie. In der Regel beziehen sich solche physiologischen Einleitungen explizit auf das menschliche Gehirn, solange es um Makrostrukturen (Hirnareale, denen Funktionen zugeschrieben werden etc.) geht. Sobald - quasi im Top-Down-Verfahren - die substrukturelle Ebene erreicht wird, werden zumeist Befunde aus Tierversuchen herangezogen, die allgemeine Aussagen auf der Makroebene experimentell untermauern sollen. Sie dienen dazu, die biologisch-physiologischen Grundlagen menschlichen Lernens, oft auch als »neuronales Lernen« gefaßt, zu vermitteln.
(3) Zwei Arbeiten aus den vierziger Jahren wurden wegweisend für die weitere Entwicklung des Konnektionismus. In "A logical calculus of the ideas immanent in nervous activity" vollzogen McCulloch und Pitts (1943) die mathematische Abstraktion von Neuronen und ihrer Verbindungen als binäre Einheiten, die in einem Folgeartikel durch analoge Einheiten ersetzt wurden (Pitts und McCulloch, 1947). Dort entwickelten sie mathematische Abbildungen für bestimmte »sensorische Inputs« und kamen auf dieser Basis zum Konzept der »topologieerhaltenden Karten«, wie es später von Kohonen (1982) genannt wurde (s.u.). Die Ausbildung solcher Abbildungen wurde als Approximationsalgorithmus in allgemeiner Form entworfen (Abb. 17, Übersetzung von uns):

Abb. 17: Rückgekoppeltes Approximationsschema aus: Pitts und McCulloch (1947, 135).
(5) Das rückgekoppelte Approximationsschema wurde bemerkenswerterweise nicht - wie später üblich - mit dem Begriff des »Lernens« belegt. Diese begriffliche Zuordnung vollzog erst Hebb (1949) in seinem Buch "The Organization of Behavior" für sein »physiologisches Lerngesetz für synaptische Modifikationen«:
(6) Nach Hebbs Vorstellung führt die gleichzeitige Aktivation zweier Neuronen zur Stärkung der Verbindungen zwischen ihnen. Zwei Neuronen werden als gleichzeitig aktiv betrachtet, wenn der Ausgangsimpuls des sendenden Neurons nahezu zum selben Zeitpunkt wie der Ausgangsimpuls des empfangenden Neurons gegeben ist. Diese umstrittene neurophysiologische Annahme, die Hebb selbst als spekulativ bezeichnet hat, wurde in verschiedenen mathematischen Fassungen als »Hebbsche Lernregel« formuliert. Sie stellt eine zentrale Grundlage konnektionistischer »Lernverfahren« dar bzw. gilt als eine Grundform der »Lernregeln« für »Neuronale Netze«. Der konnektionistische Ansatz wurde aufgrund der Verwendung des Lernbegriffs als zentralem Leitbegriff in der Folge zunehmend den behavioristischen Lerntheorien zugeordnet. So formuliert etwa Lawrence (1992), daß
(7) Während im Pitts-McCulloch-Schema ein kybernetisches Optimierungsschema für den globalen Prozeß der Approximation formuliert ist, beschreibt die »Hebbsche Lernregel« eine Anweisung, wie das globale Optimierungsschema lokal umgesetzt werden kann. Die Lokalität der »Lernregeln«, die einen globalen Effekt haben, wird als besondere Eigenschaft der »Neuronalen Netze« angesehen. Die auf dieser Basis entwickelten »Lernregeln« lassen sich in zwei große Linien einteilen, in die des »überwachten Lernens« und die des »unüberwachten Lernens«.
(8) Das »überwachte Lernen« haben wir schon in Kap. 2.3. am Beispiel des »Backpropagation«-Algorithmus vorgestellt. Hierbei handelt es sich - wie wir zeigten - um ein analytisches Approximationsverfahren, bei dem das Approximationskriterium explizit und extern gesetzt wird. Nach der mit SR-Termini vermischten Beschreibung von Kratzer (1990) könne man »überwachtes Lernen« dadurch kennzeichnen, daß
(9) Die Tendenz des Vergleichs mit menschlichen Lernprozessen, die mit dem Lernbegriff als Leitbegriff schon angelegt ist, schlägt in manchen Darstellungen in eine Vermenschlichung des Sachverhalts um. Während bei Kratzer das Netz in einer SR-Konstellation getestet und optimiert zu werden scheint und damit noch Gegenstand des menschlichen Handelns ist, ist die Darstellung von Lawrence (1992) ein Beispiel für eine vollständige Verdrehung von Subjekt und Gegenstand:
(10) Mit der »internen Repräsentation« sind in der Regel die »Aktivationen« an den verborgenen Schichten (vgl. Kap. 2.3.) gemeint, nach unserer Betrachtungsweise also die Zwischenergebnisse, die bei der Berechnung der Ausgabe zu einer gegebenen Eingabe gebildet werden. Mit dem Charakter solcher »interner Repräsentationen«, die Gegenstand scharfer Kontroversen mit VertreterInnen des klassischen KI-Ansatzes sind, setzen wir uns in Kap. 5.2. auseinander.
(11) Anhand von Beispiel-E/A-Relationen werden die Programmparameter (die »Gewichte«) sukzessiv-kumulierend optimiert. Ossen bezeichnet die Parameterapproximation daher auch als »learning by example«, da das Netz anhand von präsentierten Beispieldaten »lerne« (1990, 31). Das Resultat dieses Prozesses, bei dem das Netz durch die Präsentation von Eingabedaten »Wissen erwerbe«, wird als »Gelerntes« interpretiert. Entsprechende Formulierungen lassen sich auch bei Ritter et al. (1991) und Brause (1991) finden.
(12) Im Unterschied zum »überwachten Lernen« handelt es sich beim »unüberwachten Lernen« um ein Verfahren, das in die Klasse stochastischer Approximationsverfahren eingeordnet werden kann (vgl. Kap. 2.4., bzw. Brause, 1991, 64ff). Bei derartigen Approximationsverfahren werden Zufallszahlen zur optimierenden und zielgerichteten Berechnung neuer Parameter genutzt[25], wobei sich die Verfahren nach der impliziten Setzung der Approximationskriterien unterscheiden. Diese implizite Setzung von Approximationskriterien wird in manchen Darstellungen von KonnektionistInnen dadurch verschleiert, daß dem Netz ein Quasi-Subjektstatus zugewiesen wird. So etwa bei Kratzer (1990), der das »unüberwachte Lernen« so beschreibt:
(13) Gleichzeitig mißtraut Kratzer der Zuweisung des Quasi-Subjektstatus an das Netz und hebt hervor, daß die praktische Bedeutung solcher Netztypen gering sei,
(14) Auch für Lawrence (1992) unterscheidet sich »unüberwachtes Lernen« vom »überwachten Lernen« oder »Beispiellernen« dadurch, daß
(15) Beim »unüberwachten Lernen« hat sich der Lernbegriff gegenüber dem »überwachten Lernen« verschoben. Während das »überwachte Lernen« als von »außen« gesteuert oder als Anpassung an »äußere Bedingungen« verstanden wird und das »Lernziel« festzuliegen scheint, bleibt die Begründung des »unüberwachten Lernens« unklar. Ritter et al. (1991) fassen »unüberwachtes Lernen« als »stochastischen Prozeß« (265ff). Sie begründen das damit, daß viele »lernende Systeme« ihr Ziel durch eine Folge begrenzter Adaptionsschritte erreichen. Diese resultierten aus einer begrenzten »Interaktion« mit der »Umwelt«. Folglich hätten sie eine begrenzte »Kenntnis« über diese »Umwelt«, etwa das Eintreffen eines »sensorischen Reizes«, die sich als statistische Unsicherheit über den nächsten Adaptionsschritt äußere. Wie das »lernende System« zu dem »zu lernenden« »sensorischen Reiz« kommt (außer durch Zufall), bleibt aufgrund der stochastischen Basis der Approximationsalgorithmen unklar.
(16) Angenommen, es sei klar, daß ein »sensorischer Reiz« »gelernt« werden soll. Dieser »Reiz«, bezeichnet mit v, liegt nicht permanent und konstant vor, sondern besitzt eine Wahrscheinlichkeitsverteilung P(v). Eine Reihe von Präsentationen des »Reizes« führt zu einer Zufallsfolge von »Eingangsreizen« v und damit zu einer entsprechenden Zufallsfolge von Adaptionsschritten. Jeder Adaptionsschritt berechnet sich aus der Transformation T
(17) Die Abkürzung w steht hier für die Gesamtheit der Systemparameter, die in Analogisierung zum biologischen System als Gesamtheit der Synapsenstärken eines Netzwerkes aufgefaßt werden, und v für eine Zufallsvariable mit der Wahrscheinlichkeitsverteilung P(v). Die Simulation eines solchen »stochastischen Prozesses« liefert jedesmal nur eine seiner unendlich vielen möglichen Realisierungen (»Stichproben«). Bei genügend häufiger Wiederholung der Simulation entsteht ein »Ensemble von Realisierungen«, anhand dessen typische Realisierungen durch besonders häufiges Auftreten erkannt werden können. Das Ziel solcher stochastischer Verfahren ist nun, die Verteilungsfunktion S(w,t) der Realisierungen eines Ensembles aus unendlich vielen Simulationsläufen nach t Zeitschritten zu ermitteln. Das »Ensemble« läßt sich als eine »Punktwolke« in einem n-dimensionalen Raum auffassen und S(w,t) als Dichteverteilung der »Punktwolke« (vgl. Abb. 18 und 19, S._). Ist diese Verteilungsfunktion bekannt, so können daraus alle statistischen Eigenschaften des »stochastischen Prozesses« (sämtliche »Erwartungswerte«) berechnet werden. So können bspw. bei einem Simulationslauf aus einer Menge von Datensätzen einige charakteristische Datenpunkte als »Stellvertreter« einer jeweiligen Klasse herauskristallisiert werden, wobei jeder der Datenpunkte für ein bestimmtes Klassifikationskriterium, etwa Erwartungswert, Schwerpunkt etc. steht. Diesen Datenpunkten werden nun die anderen, davon abweichenden, Punkte innerhalb der Punktwolke zugeordnet.
(18) Insofern geht es beim »unüberwachten Lernen« als »stochastischem Prozeß« darum, die wechselseitige funktionale Abhängigkeit von Werten in einem n-dimensionalen Raum zu finden. Solche funktionalen Abhängigkeiten nennt man Korrelationen. Die gemeinsamen Kriterien der Korrelationen innerhalb einer Verteilung können rechnerisch bestimmt werden, wodurch festgelegt wird, welche Punkte innerhalb der »Wolke« zu welcher Klasse gehören. Somit ist bei diesem Verfahren die Klassifikation nicht von vornherein vorgegeben. Vielmehr ist das Ergebnis der Berechnung abhängig von der Art der Berechnung, die die Kriterien implizit setzt, und von der Wahl des »Lernobjekts« (der »Input-Daten«), dessen Herkunft - wie erwähnt - unklar bleibt. »Unüberwachtes Lernen« wird, da der Aufbau der internen Repräsentation der Ein-/Ausgabevektoren ohne Vorgabe der Klassifikation erfolgt, auch als »entdeckendes Lernen« (»learning by discovery«) bezeichnet, was die Subjektzuschreibung eher noch betont.
(19) Der in der klassischen KI-Forschung verwendete Begriff des »entdeckenden Lernens« wurde vom Konnektionismus aus Mangel eines eigenen angemessenen Begriffssystems übernommen. Die Theorie des »entdeckenden Lernens« stammt ursprünglich von Bruner (1973). Er versteht unter Entdeckung das Neuordnen oder Transformieren von Gegebenem in der Weise,
(20) Die starken Wirkungen des »entdeckenden Lernens« als Lehrmethode begründet Bruner damit, daß man dem Schüler gestattet, Dinge selbst zusammenzustellen, sein eigener Entdecker zu sein, wobei dem Lehrer die Funktion zukomme,
(21) In den folgenden Abschnitten wollen wir kurz einige Typen stochastischer Approximationsverfahren - das »Wettbewerbslernen«, die »topologieerhaltenden Karten« und die »aufmerksamkeitsgesteuerte Klassifikation« - vorstellen, ohne auf die mathematischen Grundlagen ausführlich einzugehen, da die entwickelten allgemeinen Bestimmungen aus Kapitel 2. auch hier zutreffen. Diesen Approximationsverfahren wird in der Regel größere »biologische Plausibilität« zugemessen als den analytischen Verfahren.
(22) Zur Vereindeutigung und Beschleunigung der angestrebten Klassifikation von Eingabedaten wird beim »Wettbewerbslernen« nach jedem Approximationsschritt der Ausgabewert der Einheit (»Aktivation eines Neurons«) maximiert (auf Eins gesetzt), die den schon größten Ausgabewert aufweist. Die Ausgabewerte der anderen Einheiten werden unterdrückt (auf Null gesetzt). Die Einheiten sind dabei in Clustern zusammengefaßt, die ihrerseits eine Schicht bilden. Die Einheiten innerhalb eines Clusters sind alle miteinander negativ rückgekoppelt. Die maximierte Ausgabe der aktiven Einheit unterdrückt den Aufbau hoher Ausgabewerte der anderen Einheiten des Clusters. Für diese Art der Gegenkopplung wird das in der Biologie bekannte Äquivalent der lateralen Inhibition angeführt. Rumelhart und McClelland (1986) beschreiben den Grundmechanismus dieses »Lernverfahrens« folgendermaßen:
(23) Die Gewichte werden auf Basis der »Hebbschen Lernregel« verändert, die Gewichte der gegengekoppelten Verbindung werden zusätzlich negiert. Lawrence (1992) sieht das wesentliche dieser »Lernart« darin, daß
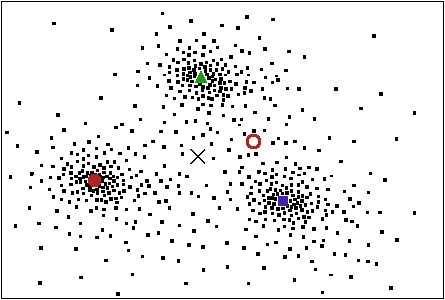
Abb. 18: Approximation von Punkteverteilungen.
(25) Was ist der Hintergrund dieser Verfahren? Mathematisch geht es um die Minimierung des Abstandes zwischen Eingabe- und Gewichtsvektor. Dabei ist mit der Netztopologie vorgegeben, wieviele Klassen den Eingabedaten zugeordnet werden können. Beispiel: Werden eine zweidimensionale Eingabedatenverteilung wie in Abb. 18, jedoch nur zwei Ausgabeklassen vorgegeben, so wird sich eine »schlechte« Approximation einstellen (verdeutlicht durch den ausgefüllten und den nichtausgefüllten Kreis), denn »offensichtlich« hat diese Verteilung drei Schwerpunkte. Sie wäre folglich mit drei Ausgabeklassen besser zu approximieren (verdeutlicht durch die ausgefüllten Symbole Kreis, Dreieck und Quadrat). Es spräche jedoch auch nichts dagegen, die Verteilung nur durch eine Ausgabeklasse zu approximieren (Kreuz), z.B. wenn aufgrund der angestrebten Anwendung eine grobe Approximation reichen würde. Klar wird hierdurch: Es hängt vom antizipierten Zweck, also vom Subjekt außerhalb des Systems, von dem/der HerstellerIn ab, welche Topologie für die jeweiligen Aufgaben gewählt werden kann. Dabei ist unerheblich, ob die Kriterien für die Approximation direkt wie in diesem Beispiel durch die Anzahl der Ausgabeklassen vorgegeben oder ob komplexere Kriterien oder übergeordnete Kriterien formuliert werden, nach denen die Approximation erfolgen soll.
(26) Bei der Analyse des Resultats der Approximation kann der mathematische Prozeß weiter erhellt werden. Bei der Approximation werden korrelierte (also voneinander abhängige) Eingabewerte in ein (im Idealfall) unkorreliertes System von Eigenvektoren[27] transformiert. Diese Transformation, in der Ingenieurwissenschaft als Hauptachsentransformation und in anderer Form in der Sozialwissenschaft als Faktorenanalyse bekannt, sei am Beispiel von Abb. 19 veranschaulicht. Die Werteverteilung ist bezüglich der Ausgangsbasisvektoren nicht separierbar, da sie sich überlagern. Wird dieses Bezugssystem nun transformiert auf das System der orthogonalen (=rechtwinkligen=unkorrelierten) Eigenvektoren (e1,e2), so ist nun eine Trennung der Verteilungen bezüglich der e1-Dimension möglich. Bezogen auf das Netz entsprechen die Gewichte nach der Approximation den (im Idealfall) unkorrelierten Eigenvektoren (vgl. auch Brause, 1991, Kap. 1.4.1, 1.4.2, 2.4). Auch hier gilt wieder: Von der Netztopologie und damit von dem/der HerstellerIn des Netzes hängt die Anzahl der Dimensionen des neuen Koordinatensystems ab, und damit, für welche Zwecke ein solches Netz eingesetzt werden kann.
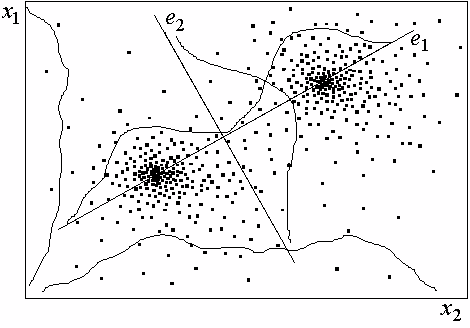
Abb. 19: Approximation von Punkteverteilungen mit dem Resultat der Hauptachsentransformation (nach Brause, 1991).
(28) Die Transformation korrelierter Eingabewerte in ein unkorreliertes System von Eigenvektoren kann auch als Wechsel der Beschreibungsebene interpretiert werden, wobei die Eigenvektoren dann die neue Basis bilden, die durch die Statistik der Daten und deren inneren faktischen Zusammenhängen bestimmt ist. Ein solches Netz mit dem »Wettbewerbslern«-Algorithmus wird daher auch als statistischer Analysator bezeichnet (Brause, 1991, 76). Da es uns um die Darstellung der Prinzipien dieses Algorithmustyps ging, haben wir problematische Aspekte (etwa die starke Reihenfolgeabhängigkeit der Musterpräsentation, Konstanz der Approximationsrate (»Lernrate«) etc.) hier ausgeklammert. Die Zerlegung in Eigenvektoren läßt sich weiterhin auch zur Datenkompression nutzen. Die Dimensionalität des Eigenvektorsystems kann geringer als die der Eingabewerte sein, sofern diese korreliert sind. Auf diese Weise kann die Redundanz in den Eingabewerten reduziert werden.
(29) Eine Modifikation des einfachen »Wettbewerbsmodells« bildet das von Kohonen (1982) entwickelte Modell topologieerhaltender Karten. Die Variation der Bezeichnungen für dieses Modell ist sehr groß: topographische Karten, selbstorganisierende Karten, topologieerhaltende Abbildungen, sensorische Karten oder einfach Kohonen-Modell. Bei diesem Modell sind die Einheiten topologisch regelmäßig angeordnet, so daß zwischen den Einheiten Nachbarschaften und Abstände eindeutig definiert sind. Wie beim einfachen »Wettbewerbsmodell« sind die Einheiten innerhalb eines Clusters miteinander rückgekoppelt. Während beim »Wettbewerbsmodell« der Ausgabewert nur einer Einheit maximiert wird ("The winner takes all"), sind die Ausgabewerte der benachbarten Einheiten beim Kohonen-Modell abhängig von einer Verteilungsfunktion. Weiterhin ist im Approximationsalgorithmus die Abnahme der Approximationsrate (»Lernrate«) vorgesehen, so daß das System bei gegebenen Eingabemustern eine Gleichgewichtslage erreicht (=Minimierung des Abstandes zwischen Eingabe- und Gewichtsvektor) und nicht mit jedem neuen Muster »pendelt« oder, wie es Brause (1991) formuliert, um zu verhindern,
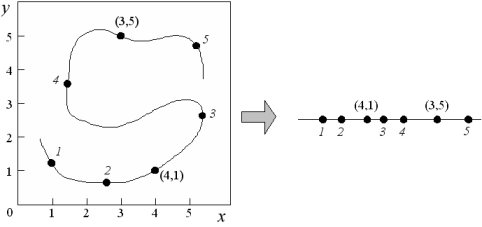
Abb. 20: Dimensionsreduktion am Beispiel eines Pfades auf einer Fläche.
(31) Wie schon beim einfachen »Wettbewerbsmodell« kann auch hier die Dimensionalität der Eingabewerte reduziert werden, zusätzlich jedoch bleibt bei einer Approximation die Nachbarschaft der Punkte des Eingabesystems im Ausgabesystem erhalten. Abb. 20 zeigt ein einfaches Beispiel der Abbildung eines durch zwei Parameter beschriebenen »Pfades« auf einer Ebene (2-D) auf einen nur noch durch einen Parameter beschriebenen korrespondierenden »Pfad« auf einer Strecke (1-D). Die Erhaltung der Nachbarschaftsbeziehungen der Punkte auf dem »Pfad« in der eindimensionalen Repräsentation hat den Vorteil, daß die Reihenfolge der Punkte eindeutig bestimmbar ist (etwa: Nachfolgende Punkte auf dem »Pfad« haben größere Werte auf der Strecke.), während dies aus den Parameterpaaren der zweidimensionalen Repräsentation des »Pfades« nicht einfach ermittelbar ist (etwa: Liegt (3,5) vor oder hinter (4,1)?).
(32) Interessant sind solche topologieerhaltenden Karten für die Reduktion höherdimensionaler Signale auf zweidimensionale Karten. So hat Kohonen (1988) ein solches Netz verwendet, um akustische Spektren finnischer Sprachphoneme auf eine zweidimensionale Karte so abzubilden, daß klangähnliche Phoneme auf der Karte auch benachbart sind. Eine solche Karte kann bspw. für Sprachanalysesysteme eingesetzt werden.
(33) Trotz verschiedener Zuschreibungen wie etwa der »Selbstorganisation« solcher Netze (vgl. Lawrence, 1992, 91, Ritter et al., 1990, 61ff, Kohonen, 1982), die einen Eigenständigkeits- oder Quasi-Subjektstatus des Netzes nahelegen, ist dennoch die Aufgabe der das Netz herstellenden und benutzenden Person benennbar: Sie bestimmt sowohl die Auswahl der Eingabemuster (bzw. des zu modellierenden Sachverhalts) als auch die Konfiguration und Optimierung des Approximationsprozesses (insbesondere über die Bestimmung der Abnahmefunktion für die Approximationsrate, die als »Lernrate« bezeichnet wird) von »außen«. Sofern topologieerhaltende Karten innerhalb von Werkzeugen eingesetzt werden (Sprachanalysesysteme, Robotersteuerungen etc.), erscheinen die genannten Zuschreibungen also eigentlich unnötig. Wie ist es aber bei der Modellierung biologischer Prozesse? Kohonen maß seinem Modell eine entscheidende physiologische Plausibilität bei, denn:
(34) Topologischen Karten wird demnach eine wichtige Erklärungspotenz dafür zugesprochen, wie aus unspezifischen »Reizen« »bedeutsame Einheiten« werden. Hier wird bei Tieren die Ebene des Verhältnisses zur Umwelt bzw. bei Menschen die des Verhältnisses zur Welt angesprochen, also jeweils die spezifische Ebene des Lebens. Andererseits werden topologieerhaltende Karten sehr oft auch benutzt, um eher unspezifische Ebenen des Lebens abzubilden, etwa als sensorische oder motorische Karten zur (unbewußten) Perzeption oder Bewegungssteuerung. Auf beiden Ebenen werden also die gleichen Modelle und wird vor allem der gleiche Lernbegriff verwendet. Die Angemessenheit solcher verallgemeinernden Anwendungen des konnektionistischen Lernbegriffs wollen wir ausführlich am Beispiel der Okulomotorik (unbewußte Augenbewegung als Beispiel eines unspezifischen Prozesses) und des Lernens der Vergangenheitsform englischer Verben bei Kindern (einer spezifisch menschlichen Handlung) in Kapitel 5.1. nachgehen.
(35) Dieses Modell geht auf Arbeiten von Carpenter und Grossberg (1987) zurück. Die von ihnen entwickelte Netztopologie und der verwendete Algorithmus werden als Adaptive Resonanz-Theorie (ART) bezeichnet. Das Netz besteht aus zwei Schichten, der Eingabeschicht und einer Speicherschicht (Ausgabeschicht), die wie beim »Wettbewerbsmodell« innerhalb der Schicht jeweils negativ rückgekoppelt vernetzt sind. Andererseits erfolgt die Vermittlung von Schicht zu Schicht wie bei den unidirektionalen Netzen (feed-forward).
(36) Um das schon beim Kohonen-Modell angesprochene Plastizitäts-Stabilitäts-Dilemma (schnelle, aber schwankend-unstabile versus langsame, aber stabile Approximation) zu beseitigen, wird ein Parameter der "Aufmerksamkeit" zur "Kontrolle der Klassifizierung" (Brause, 1991, 154) eingeführt. Bei dem Modell zur »aufmerksamkeitsgesteuerten Klassifikation« (wir beziehen uns hier auf das Modell ART1) werden die »Muster« erst nach einer »Ähnlichkeitsprüfung« gespeichert. Die Approximation und Veränderung der Gewichtsparameter finden hier nur dann statt, wenn ein neues »Muster« mit einem bereits gespeicherten genügend übereinstimmt und daraufhin das gespeicherte anhand des neuen »Musters« in geeigneter Weise geändert wird. Ist die »Ähnlichkeit« gemäß der Vorgabe gegeben, so können die durch den folgenden Approximationsschritt veränderten Parameter (Gewichte) die Klasse stabilisieren (in Resonanz bringen). Ist die »Ähnlichkeit« zu klein, wird stattdessen eine neue Klasse erzeugt und das abweichende »Muster« als ihr Klassenprototyp gespeichert. Die kurzfristige Aufnahme eines »Musters« in die erste Schicht wird in Anlehnung an kognitivistische »Mehrspeichermodelle« als »short term memory trace« STM bezeichnet. Die Parameter (Gewichte), die sich nach Ähnlichkeitsprüfung und Klassifikation durch die zweite Schicht einstellen, werden auch als »long term memory trace« LTM bezeichnet. Für Brause handelt es sich bei der Zuordnung zu einem bestehenden Klassenprototypen um »langsames Lernen« und bei der Bildung einer neuen Klasse um »schnelles Lernen«:
(37) Ähnlich beschreibt auch Grossberg (1982) den Vorgang. Er bezeichnet die geringen Gewichtsänderungen, die einen stabilen Zustand des Netzwerks hervorrufen, auch als langsame Veränderungen des »Langzeitgedächtnisses«, in das die im »Kurzzeitgedächtnis« gespeicherten »Muster« aufgenommen würden. Die Folgeversionen der ART-Modelle wurden um zusätzliche Parameter und Funktionen erweitert, so ART2 um eine Funktion zur Bildung eines »erwarteten Musters« (eine Art Muster-Antizipierer), das als Vergleich dient. Alle Modifikationen dienen dazu, grundsätzliche bei der Musteranalyse immer auftretende Probleme in den Griff zu bekommen, so das Verhältnis von neuen und gespeicherten Mustern, die Erreichung eines stabilen Zustandes ("Resonanz") für eine Klasse, die Definition von Klassengrenzen etc. Carpenter und Grossberg versuchten, mit den ART-Netzen ein plausibles Modell der Wahrnehmung zu schaffen, wobei der Parameter der »Aufmerksamkeit« sprachliche und konzeptionelle Verbindung zu menschlichen (oder tierischen) Aufmerksamkeitsprozessen zu schaffen versucht. Von der Bedeutung des zu Erkennenden wird abstrahiert bzw. implizit wird angenommen, die figuralen Qualitäten der Dinge alleine ließen eine Einteilung in für das Individuum relevante Klassen zu. Ähnlich wie bei Kohonen besteht also die Vorstellung, daß die Bedeutung (die Bildung semantischer Items, wie Kohonen sagt) als Abbildung formuliert und unabhängig vom Individuum der Außenwelt als Eigenschaft quasi-objektiv zugeordnet werden könne. Lernen ist demnach der Prozeß der Realisierung einer Abbildung.
(38) Analytische bzw. stochastische Approximationsverfahren werden im Konnektionismus als »überwachtes Lernen« bzw. »unüberwachtes Lernen« bezeichnet. Diese begriffliche Fassung ist in mehrfacher Hinsicht problematisch.
(39) Dem besonderen Charakter konnektionistischer Verfahren als kumulative Optimierung der Systemparameter zur generalisierenden Approximation von Funktionen, die gewünschte E/A-Relationen widerspiegeln, wird nicht entsprochen. Hierbei ist das Verhältnis von notwendigen mathematischen Anstrengungen und einer entsprechenden Begrifflichkeit vielfach gebrochen. Der verwendete Begriff des »Lernens« soll vor allem den globalen Prozeß der kumulierend optimierenden Parameterapproximation in den (Be-)Griff bekommen, da sich eine mathematische Formel des globalen Prozesses bei größeren Netzen nicht mehr sinnvoll aufschreiben läßt. Eine solche Formel läßt sich nur für einen lokalen Approximationsschritt formulieren, die dann, als Ableitung aus den optimierenden globalen Systemeigenschaften, als »Lernregel« aufgefaßt wird. Die lokale Approximationsregel als einfache Rekursionsvorschrift legt eine Analogie zum »Lernen« zunächst keinesfalls nahe.
(40) So war es historisch etwa möglich, kybernetische Regelkreisläufe ohne Bezug auf einen Lernbegriff theoretisch zu begründen. Der Unterschied von Kybernetik und Konnektionismus ist das Analogon: Die Kybernetik war eine Abstraktion von industriell-maschinellen Regelprozessen, wo es offensichtlich nicht um ein »Lernen von Systemen« ging, sondern um das »Regeln der Systeme«; der Konnektionismus war hingegen als Abstraktion neurophysiologischer Prozesse sehr unmittelbar mit einer Analogie des »lernenden Verhaltens« der modellierten Lebewesen verbunden. Stand zu Beginn der Herausbildung des Konnektionismus die Modellbildung als Instrument des Verstehens der untersuchten neurophysiologischen Prozesse im Vordergrund (vgl. etwa McCulloch/Pitts, Hebb), so drehte sich das Verhältnis von Gegenstand und Modell spätestens ab dem Perceptron (Rosenblatt, 1958) um. Nun war das implementierte »lernende künstliche System« der Forschungsgegenstand, während reale neurophysiologische Prozesse vor allem als Modell oder Vorbild für das künstliche System untersucht wurden. Die originäre Neurophysiologie bestand natürlich weiter, das Verhältnis zur Computerwissenschaft kippte aber um, was Konsequenzen für die Methodologie und Begrifflichkeit innerhalb der im engeren Sinne neurophysiologischen Forschung hatte. Die physiologische Forschung orientierte sich zunehmend an durch die Computerwissenschaft vorgegebenen Kategorien (z.B. dem Begriff der »Informationsverarbeitung«). Die konnektionistische Computerwissenschaft übernahm umgekehrt selektiv passende Ausschnitte der neurophysiologischen Terminologie, z.B. auch den Lernbegriff (dessen ebenfalls problematische Verwendung innerhalb der Neurophysiologie ein anderes Thema ist). Der Lernbegriff wurde zum Universalbegriff im Konnektionismus und zum modischen Werbeleitbegriff in der Konkurrenz um Forschungsgelder wie etwa der Intelligenzbegriff der klassischen KI-Forschung.
(41) Die Bezeichnungen des »überwachten« bzw. »unüberwachten Lernens«, wie sie im Konnektionismus zur Unterscheidung verschiedener Approximationsverfahren verwendet werden, werfen vielleicht ein Licht auf die gängige Vorstellung menschlichen Lernens[29], tragen jedoch zum Verständnis des Konnektionismus wenig bei. Während der Terminus des »Überwachens« noch nahelegt, außerhalb des Systems gäbe es eine/n, die/der das System kontrolliert, steuert, also für ihre/seine Zwecke einsetzt, ist mit dem Begriff des »Unüberwachten« eine Vorstellung des »selbstaktiven« Systems verbunden. Solche Systeme, in denen der intendierte Zweck nicht direkt als Approximationsgütekriterium vorgegeben ist, sondern weniger offensichtlich als implizites Kriterium (Netztopologie, Auswahl der Objekte etc.) gesetzt ist, werden oft mit dem irreführenden Begriff des »selbstorganisierenden Systems« belegt. Werden Bezeichnungen wie die der Selbstorganisation und des Lernens in einem kausal-logische Strukturen verschleiernden Sinne verwendet, so ist das dem Gegenstand nicht angemessen und behindert zudem die Durchdringung des gegebenen Sachverhalts. Wir nehmen hier als Beispiel unsere eigenen Erfahrungen mit einer Vorlesung "Einführung in den Konnektionismus" 1991 an der TU Berlin, in der wir uns im Verhältnis zum dargebotenen »Stoff« widerständig und mühselig zum Kern der Sache vorarbeiten mußten. Die Auseinandersetzung mit dem eigenständigen Konzept der »Selbstorganisation« als »Kybernetik der Kybernetik« oder »Kybernetik zweiter Ordnung« (von Foerster, 1993) und den erkenntnistheoretischen Grundlagen des Konstruktivismus können wir an dieser Stelle nicht führen.
(42) Ausgangspunkt unserer Kritik ist die Vorstellung von »Lernen« als Approximationsprozeß eines Netzwerkes entweder anhand von außen vorgegebenen Anforderungen (wie beim »überwachten Lernen«) oder anhand von implizit gesetzten Kriterien (wie beim »unüberwachten Lernen«), die nur scheinbar auf eine »Eigenaktivität« des Netzes verweisen. Diese Approximations- bzw. Optimierungsprozesse sollen abbildbar sein und ohne bewußte Intentionen von Subjekten außerhalb des Systems ablaufen. »Selbstorganisation« und »Selbstoptimierung« erfolgen gemäß dieser Vorstellung also nicht von einem »Selbst« außerhalb des Systems, sondern vom »System selbst«. Damit ist jedoch eine unspezifische Ebene der Optimierung unterhalb des psychologischen Niveaus menschlicher Subjektivität angesprochen. Die Tatsache, daß es sich nur um eine unspezifische Ebene handeln kann, wird verkannt und als Erkenntnis verunmöglicht, indem dem Netzwerk Subjektcharakter zugesprochen wird. Das hat zwei Konsequenzen. Zum einen bleibt dadurch verborgen, daß über intendiertes Lernen noch gar nichts ausgesagt wurde, zum anderen kann das Verhältnis zwischen intendierten Lernhandlungen und unspezifischen Optimierungsprozessen, die in konnektionistischen Netzwerken tatsächlich abgebildet werden können (vgl. Kap. 5.1.), erst gar nicht zum Problem werden. In den gängigen Konzepten gibt es schlicht keine Unterschiede - alles ist »Lernen«. Durch diese Verallgemeinerung wird der Umstand verschleiert, daß von menschlichem Lernen - das ein Subjekt voraussetzt, das lernt - überhaupt nicht die Rede ist und nicht sein kann (wir kommen darauf in Kap. 5.1. zurück).
(43) Darüber hinaus sind die den konnektionistischen Netzwerkmodellen zugrundeliegenden Vorstellungen von »Lernen« im begründungstheoretischen Kontext betrachtet in mehrfacher Hinsicht problematisch. In der generellen Auffassung von »Lernen« als Approximationsprozeß anhand von vorgegebenen oder durch die Netztopologie, die Auswahl der Objekte etc. implizit gesetzten Kriterien ist »Lernen« immer nur in seiner »fremdbestimmten Form« erfaßbar. Dies wird besonders an der Konzeption des »überwachten Lernens« sichtbar, bei dem ein (implementierter) »Lehrer« Vorgaben macht und das »Verhalten« des Netzes anhand von externen Maßstäben »überprüft«. Diese Vorstellung entspricht der gängigen Auffassung, daß menschliches Lernen bereits dann zustande kommt, wenn von dritter Seite entsprechende Lernanforderungen gestellt oder von irgendwelchen dafür zuständigen Instanzen geplant werden. Jedoch:
(44) »Fehler« regulieren hier auch nicht automatisch den Lernprozeß, wie bspw. im Konzept des »Backpropagation« nahegelegt und in SR-theoretischen Ansätzen angenommen (qua »Verstärkung«). Vielmehr müssen Subjekte das, was von der Anforderungsseite als »Fehler« zurückgemeldet wird, erst einmal als ihr Kriterium übernehmen, ehe sie im Kontext ihrer Lernproblematik ihre Handlungen daran orientieren. Die Gleichsetzung von »fremdbestimmtem« Lernen mit Lernen überhaupt verdeutlicht sich auch an der Übernahme von Bruners Theorie des »entdeckenden Lernens«, dergemäß die Lehrer durch diese Lehrmethode den SchülerInnen nach didaktischen Gesichtspunkten bestimmte Freiheitsgrade beim Entdeckungsprozeß zugestehen und sie so zu »spontanen« Denkern machen. Danach sollen die SchülerInnen das »entdecken«, was der Lehrer selbst ja schon kennt. Dieser gibt ihnen entweder »Rätsel« auf, deren Lösung er schon weiß, oder er läßt sie im unklaren darüber, daß das von SchülerInnen zu Entdeckende ihm bereits bekannt ist (vgl. ebd., 421f). Eine solche Analogie »paßt« natürlich zum »entdeckenden Lernen« bei »Neuronalen Netzen«. Sie sagt jedoch allenfalls etwas über die eingeschränkten Vorstellungen vom menschlichen Lernen aus als über die Qualität konnektionistischer Approximationsverfahren.
(45) Individuen werden nur als Objekte fremder Einwirkung betrachtet, nie als Ursprung eigener (Lern-)Handlungen. Ihre »Selbstorganisation« ist somit immer nur als Erfüllung fremdgesetzter Anforderungen denkbar. Auf diese Weise kann Lernen nie als Problematik vom Standpunkt des Subjekts begriffen, präziser: kann intentionales Lernen vom Subjektstandpunkt als subjektiv begründete Übernahme einer Handlungsproblematik als Lernproblematik erst gar nicht zum Thema werden. So bleiben viele von uns im begründungstheoretischen Lernkonzept aufgewiesene Aspekte, Verlaufsformen und Erscheinungsweisen des lernenden Weltentdeckens unkenntlich. Intentionales Lernen findet nie ohne Lernproblematik statt. Ein Lernen ohne Lernproblematik wäre gleichbedeutend mit subjektlosem Lernen. Insofern widerspiegeln konnektionistische »Lernkonzepte« die realen Prozesse in einem Netz: Dieses »lernt« nicht(s), da »es« kein Subjekt ist. Genau diese Tatsache aber wird gleichzeitig dadurch verschleiert, indem dem Netzwerk Subjektcharakter zugesprochen wird. Mit den »Lernkonzepten« wird also vorgegeben, etwas zu tun, was sie nicht tun können, was sie wiederum, weil sie es nicht wissen, daß sie es nicht tun können, auch nicht bemerken. Jemand, der in der Wüste geradeaus laufen will, um ein Ziel zu erreichen, dabei aber immer im Kreise läuft und dieses nicht bemerkt, kann sich einreden: Ich habe mein Ziel nicht erreicht, aber ich komme ihm immer näher. Der Kreisläufer geht davon ausgeht, daß er sich dem Ziel annähert, weil er läuft, denn seine Hypothese lautet: wenn ich laufe, dann komme ich meinem Ziel näher.
(46) Der Konnektionismus geht davon aus, das seine Systeme lernen, weil sie funktionieren, denn seine Hypothese lautet: wenn die Approximationsalgorithmen funktionieren, dann lernen die Systeme. Und der wirkliche Mensch? Kein Lerngegenstand, kein Handlungszusammenhang, keine Lerngründe - wie erklären sich KonnektionistInnen das menschliche Lernen? Logisch bleibt da nur übrig: Ein Subjekt lernt, weil es lernt.
(47) Wir hatten in Kap. 4.2. gezeigt, daß zu einer Lernhandlung immer ein Lerngegenstand gehört, in dessen Bedeutungsstruktur das Lernsubjekt praktisch eindringt, wobei stets schon bestimmte Prozesse des Vorlernens vorausgesetzt sind. KonnektionistInnen versuchen zwar, Netzwerkmodelle mit der Realität in Beziehung zu setzen. Indem sie diese Realität jedoch auf programmsprachlich repräsentierte Umweltreize reduzieren, werden auch diese »Lerngegenstände« ihrer Bedeutung beraubt. Sie können nur noch als isolierte Einzelereignisse, die mit einer bestimmten Wahrscheinlichkeit auftreten, gefaßt werden. In diesem Sinne entspricht die konnektionistische Auffassung von »Lernen« dem »induktiven Lernen«, bei dem zufällige Regelhaftigkeiten von Ereignisfolgen gelernt werden (s. S._)[30]. Da somit Bedeutungsstrukturen eines Lerngegenstands auf isolierte Einzelereignisse reduziert werden, ist auch ein »praktisches Eindringen« in diese Bedeutungsstrukturen, indem diese durch ihnen adäquate Bewegungen realisiert werden, nicht denkbar. Beim Versuch, ein derartiges »Eindringen« dennoch abzubilden (etwa durch einen mit Sensoren ausgestatteten Roboter, der »Hindernisse« umgeht etc.), können dann nur formalisierbare und regelbare bzw. operationalisierbare Aspekte einer Bewegung einerseits und raumzeitliche Strukturen bzw. figural-qualitative Merkmale eines Gegenstands andererseits abgebildet werden.
(48) Bedeutungen konstituieren sich jedoch weder aus figural-qualitativen Merkmalen noch aus raumzeitlichen Strukturen (vgl. Kap. 3.2.). Die operationalisierbaren Aspekte einer Bewegung sind auch nicht gleichbedeutend mit der individuell-antizipatorischen Aktivitätsregulation, um die es sich beim regulatorischen Lernaspekt handelt, da solche Aktivitätsregulationen immer auf einen übergeordneten Handlungszusammenhang bezogen sind, von dem in Netzwerkmodellen jedoch abstrahiert wird (vgl. zum Verhältnis von Handlung und Operation, S._). Somit können konnektionistische »Lernkonzepte« den inhaltlich-bedeutungsbezogenen Aspekt der Handlung, den wir als thematischen Lernaspekt bezeichnet haben, nicht abbilden. Die Modellierung des operativen Lernaspekts ist dann unterbestimmt, wenn der Zusammenhang zum thematischen Lernaspekt ausgeblendet wird.
(49) Weiterhin schließt die Vorstellung vom »Lernen« als Approximationsprozeß lediglich kontinuierliche »Lernfortschritte« ein, nicht jedoch qualitative »Lernsprünge«. Dies verdeutlicht sich bspw. daran, daß im Approximationsalgorithmus lediglich eine als »Lernrate« bezeichnete Approximationsrate vorgesehen ist, die zu-, abnimmt oder gleichbleibt, in jedem Fall aber selbst der Optimierungsanforderung unterliegt. Die konnektionistische »Lernkonzeption« verfehlt somit in zentralen Aspekten den Gegenstand. Sie erfaßt »Lernen« im wesentlichen als Anpassungsprozeß an (implizit oder explizit) vorgegebene Bedingungen, damit immer nur in seiner Außendetermination.
(50) Von der Einschätzung, daß die Funktionenapproximation als »Lernprozeß« inadäquat begrifflich gefaßt ist, zu trennen ist die Frage nach der Potenz des Konnektionismus, Prozesse unterhalb der Ebene subjektiv-intendierter Lernhandlungen modellieren zu können. Diese Möglichkeit ist unserer Auffassung nach durchaus dann gegeben, wenn solche Prozesse nicht zu Lernprozessen verklärt werden und wenn die Differenz von Modell und Modelliertem theoretisch erhalten bleibt. Letzteres ist nur dann gegeben, wenn in der Wissenschaftssprache des Konnektionismus die Vorstellung eines »selbstaktiven« Systems überwunden wird. Von der Kritik an der Verwendung des Lernbegriffes ebenfalls nicht betroffen ist die Möglichkeit, konnektionistische Systeme für gesellschaftliche Zwecke zu bauen, sie also als Werkzeuge zu nutzen. Die Unangemessenheit eines Lernbegriffs erscheint hier, da das BenutzerIn-Werkzeug-Verhältnis in der Werkzeugperspektive eingeschlossen ist, von einer »Eigenständigkeit« des Systems also nicht die Rede ist, noch unsinniger. Zumeist sind beide Perspektiven, die Modellierungsperspektive und die Werkzeugperspektive, miteinander vermischt, da angenommen wird, durch eine geeignete Modellierung physiologischer oder/und kognitiver Prozesse, die Leistungsfähigkeit der Werkzeuge zu verbessern. Um eine Vermischung von Potenzen und Verschleierungen in der Theoriebildungsphase zu vermeiden, ist es sinnvoll, die Perspektive der Modellierung unspezifisch-physiologischer (u.U. auch physikalischer oder bloß statischer) Prozesse aus Gründen des Erkenntnisgewinns über den modellierten Gegenstand von der Perspektive der Konstruktion konnektionistischer Werkzeuge zur Erfüllung menschlicher Bedürfnisse zu trennen. Eine solche konzeptionelle Trennung schließt nicht aus, vertiefte Kenntnisse über Naturzusammenhänge für menschlich-gesellschaftliche Zwecke z.B. in Form konnektionistischer Werkzeuge nutzbar zu machen - es liegt ja gerade in der menschlichen Natur, dies tun zu können.
(51) Ein weiterer Aspekt ist die Wirkung einer Disziplin in der nicht-akademischen Öffentlichkeit. Es ist unseres Erachtens nicht begründbar, scheinbar einfachere Begriffe wie den des Lernens zur populären Vermittlung zu verwenden. Die Einfachheit macht sich nicht an einer gelungenen Analogie fest (hier ist sie zudem deutlich mißlungen), sondern an der Möglichkeit, mit den verwendeten Begriffen den Kern der Sache durchdringen zu können. So spräche nichts dagegen, etwa auf Basis des Begriffs der Approximation (oder Annäherung) den Konnektionismus auch allgemeinverständlich darstellen zu können. Das Verhältnis zur Neurophysiologie muß dabei nicht ausgeblendet werden, es müßte als das thematisiert werden, was es ist: als problematisches Verhältnis (vgl. Kap. 5.1.).
(52) Der Konnektionismus betrachtet Lernen in erster Linie als eine Verknüpfung von »Reiz« und »Reaktion«, die er auch als »assoziatives Lernen« bezeichnet, das klassisches und operantes Konditionieren umfaßt. Durch die starke Nähe seiner »Lernverfahren« zum Behaviorismus stellt sich somit die Frage, ob der Konnektionismus, obwohl im Kontext des Kognitivismus entstanden, inhaltlich nicht angemessener als eine Computerisierung SR-theoretischer Lernkonzepte bestimmt werden könnte. Dies scheint nicht nur dadurch gerechtfertigt, daß in der konnektionistischen Wissenschaftssprache die bedeutungsvolle Welt durch die Verwendung des Reizbegriffs in organismischen Termini gefaßt wird, sondern unter anderem auch dadurch, daß er in seiner Modellbildung von einem abstrakten, ahistorischen Organismus ausgeht, auf den irgendwelche (dann programmsprachlich gefaßten, unterschiedlich quantifizierten) Umweltreize unmittelbar wirken. Damit werden sowohl qualitative Entwicklungsunterschiede der Lernfähigkeit zwischen Tieren und Menschen als auch innerhalb der tierischen Spezies selbst nivelliert. Diese Entwicklungsunterschiede erscheinen lediglich als quantitative Unterschiede der »Lernkapazität« verschiedener Organismen. Damit werden auch die qualitativen Besonderheiten der artspezifischen Umwelt sowie der gegenständlich bedeutungsvollen Welt eliminiert. Der Konnektionismus kennt somit nur elementare Verknüpfungseinheiten (wie klassisches Konditionieren, operantes Konditionieren) sowie gewisse für alle Organismen gleichermaßen gültige Gesetzlichkeiten des »lernabhängigen« Verhaltensaufbaus aus diesen Verknüpfungseinheiten.
(53) Die starke konzeptionelle Verbindung zum Behaviorismus verdeutlicht sich auch an den verschiedenen Spielarten der »Verstärkung« von Netzeffekten: So etwa im Kontext des »überwachten Lernens«, bei dem die Gewichtungen eines Netzes in Abhängigkeit von ihrer Beteiligung am Ergebnis solange modifiziert werden, bis das Netz den gewünschten Effekt zeigt, d.h. den gewünschten »Output« produziert, oder im Kontext des »unüberwachten Lernens« als stochastischem Prozeß, bei dem genügend häufige Wiederholungen der Simulation von »Eingangsreizen« zu einer Auftretenshäufigkeit von bestimmten Adaptionen führen. Beim »Wettbewerbslernen« wird vor allem die Einheit innerhalb eines Clusters verstärkt, das die größte Aktivation besitzt und den maximalen Ausgangswert annimmt, wobei die Verstärkung darin besteht, Gewichtungen so umzuverteilen, daß sich schließlich nur eine Lösungskonfiguration durchsetzt. Es werden also bestimmte Effekte verstärkt und diese zu »Erfahrungen des Netzes« verallgemeinert. Die Verstärkung bestimmter Effekte geschieht im Hinblick auf die Anpassung des Netzes an ein gewünschtes Ergebnis. Betrachtet man die Verstärkungskonzepte von dem Hintergrund, daß Netzwerkoptimierungen zu »Lernprozessen« überhöht werden, wird auch hier die Auffassung deutlich, daß »Lernen« eine Anpassung an vorgegebene Erfordernisse sei. Menschen werden somit - wie im Behaviorismus - lediglich als unter Bedingungen stehend begriffen, an die sie sich anpassen.
(54) Diese reduktionistische Auffassung von »Lernen« als Anpassung an in organismischen Termini gefaßte sachlich-soziale Bedeutungszusammenhänge, die auf (programmsprachlich repräsentierte) quantifizierbare Umweltreize reduziert werden, die damit verbundene Abstraktion von der handelnden und lernenden Möglichkeitsbeziehung des Menschen teilt der Konnektionismus mit dem Behaviorismus. Obwohl beide somit von gleichen Voraussetzungen ausgehen, gelangt der Konnektionismus im Versuch, seine Modelle mit der Realität in Beziehung zu setzen, auf derselben Grundlage zu anderen theoretischen Konzepten, wie wir sie mit den »Lernverfahren« dargestellt haben. Allerdings wird der behavioristische Rahmen nicht überschritten. Die Forschungsrichtung der »Neuronalen Netze« ist somit nur bedingt dem Kognitivismus zuzuordnen.
(55) Während das äußerlich beobachtbare »Verhalten« des Netzes in SR-theoretischen Termini beschrieben wird, wobei »Stimuli« und »Responses« als »Verhaltenselemente« des Netzes angesehen werden, werden Gedächtnisfunktionen in kognitivistischen Termini gefaßt. Dabei wird (wie im von uns dargestellten Carpenter-Grossberg-Modell) auf kognitivistische Mehrspeichermodelle zurückgegriffen, die im Zuge der Entwicklung der Informatik wieder modern wurden. So etwa, wenn angeblich Informationen speichernde Gewichtungen mit dem Terminus »Langzeitgedächtnis« und Speicherungs- sowie Klassifikationsprozesse in der Speicherschicht mit dem Terminus »Kurzzeitgedächtnis« bezeichnet werden. Durch die Hineinverlagerung von Subjekten in das Netzwerksystem werden menschliche Behaltensleistungen mit Speicherleistungen des Netzes gleichgesetzt und diese als Eigenschaft des jeweiligen Speichers betrachtet. Damit werden auch hier Speicher zu Subjekten des Transfers von Informationen. Der Speichern zugeschriebene Subjektcharakter kommt vor allem auch darin zum Ausdruck, daß »ihnen« Bewußtsein unterstellt wird, aufgrund dessen sie in der Lage sind, aufmerksamkeitsgesteuert und anhand von Ähnlichkeitskriterien Klassifikationen vorzunehmen und zu speichern. Dabei bleibt verborgen, daß von einem menschlichen Gedächtnis, das ein wirkliches Subjekt mit seinen biographisch gewordenen Weltbeziehungen vorsieht, nicht die Rede ist. Meine Art des Erfahrungsgewinns und Weltwissens ist nicht zu lösen von meinen konkret-historischen Beziehungen zur sachlich-sozialen Welt. Mein Weltwissen ist dabei nicht nur auf mentale Wissensstrukturen begrenzt, sondern diese enthalten vielfältige Verweisungen auf kommunikative und objektivierende Organisationsformen. In diesem Sinne hatten wir Wissen als modalitätsübergreifende Verweisungsstruktur gefaßt (vgl. S._). Die konnektionistische Gedächtniskonzeption kennt jedoch nur im Netz fixierte »Gedächtnisarten«, die bestenfalls eine Modellierung kognitivistischer Mehrspeichermodelle darstellen, deren Problematik wir bereits aufgewiesen haben. Während dort jedoch noch Subjekte vorausgesetzt sind, sind sie hier völlig eliminiert. Damit kann nichts über intendiertes Behalten/Erinnern sowie entsprechende modalitätsübergreifende Strategien ausgesagt werden.
(56) Die verschleiernde Hineinverlegung des Subjekts in das System kann nur dadurch aufgehoben werden, daß der reale Subjektstandpunkt von Individuen außerhalb des Systems theoretisch erkannt und integriert wird. Die Überwindung des »introjektiven« Systemsubjekts bedeutet zunächst einmal eine Aufhebung der Computer- bzw. Netzwerkanalogie, in dem man sich klarmacht, daß Menschen Computersysteme oder auch Netzwerke für bestimmte verallgemeinerte Zwecke herstellen, die somit Mittelfunktion zur Bewältigung bestimmter Aufgaben haben. Wird auf diese Weise die »Mittelperspektive« oder Benutzungsperspektive wieder zurückgewonnen, kann auch die handelnde und lernende Möglichkeitsbeziehung des Menschen zur Realität wieder in den Blick geraten. Wir hatten herausgearbeitet, daß gegenständliche Bedeutungen - und ein Netzwerk hat eine von Menschen geschaffene Gegenstandsbedeutung - dem einzelnen Individuum immer nur als Handlungsmöglichkeiten gegenüberstehen, die es als seine Möglichkeiten realisieren kann oder auch nicht. Dabei impliziert die Realisierung dieser Möglichkeiten immer schon eigene Lernprozesse. Insofern kann ich ein Netzwerk auch als potentiellen Lerngegenstand betrachten, in den nur ich als Subjekt lernend eindringen kann - unter Berücksichtigung meiner Verfügungsinteressen und unter der subjektiven Voraussetzung, daß ich mit Bezug auf ein Netzwerk mehr lernen kann als mir jetzt schon zugänglich ist.
(57) [24] Engl. Original: "When an axion of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased".
(58) [25] Die Monte-Carlo-Verfahren, bei denen durch Trial-And-Error versucht wird, zufällig (also nicht optimierend zielgerichtet) die beste Lösung zu finden, seien hier ausgeklammert.
(59) [26] Engl. Original: "Every element in every cluster receives inputs from the same lines. A unit learns if and only if it wins the competition with other units in its cluster. A stimulus pattern Sj consists of a binary pattern in which each element of the pattern is either active or inactive. (...) If a unit does not respond to a particular pattern, no learning takes place in that unit. If a unit wins the competition, then each of its input lines give up some proportion g of its weight and that weight is then distributed equally among the active input lines."
(60) [27] Begriff und Bedeutung des Eigenvektors kann an dieser Stelle nicht weiter ausgeführt werden (vgl. z.B. Brause, 1991).
(61) [28] Engl. Original: "If the ability to form maps were ubiquitous in the brain, then one could easily explain its power to operate on semantic items", was zu der Frage führe, "... how symbolic representations for concepts could be formed automatically".
(62) [29] Etwa die Vorstellung, »Lernen« wäre überwachbar, von außen steuerbar oder determinierbar; vgl. dazu zum Verhältnis von subjektiven Lerninteressen und äußerem (institutionellen) Zwang Holzkamp, 1987.
(63) [30] Insofern stimmt die von der klassischen KI-Forschung übernommene Charakterisierung des »Beispiellernens« (»learning by example«) und des »entdeckenden Lernens« (»learning by discovery«) als »induktives Lernen« (vgl. Ossen, ebd., 37).
Zurück: 4.3.2. Der Kognitivismus
Vor: 5. Reichweite und Grenzen der Theorie »Neuronaler Netze«